Benchmarking quantum computers to compare their capabilities becomes increasingly important as the technology moves to market. In a master’s thesis supervised by Kvantify, we gave the benchmarking problem a shot.
Let’s imagine the following scenario: A quantum hardware provider, a quantum software provider and a business owner walk into a meeting room. The business owner has a certain problem that he wants to solve on a quantum computer. The quantum software provider ensures him that this is indeed possible using so and so many qubits. They both turn to the quantum hardware provider, who details the size of their system and quality of their qubits.
At the end of the meeting the business owner is intrigued, but it is not clear to him whether it is the best solution. So, the quantum software provider arranges a meeting with a new quantum hardware provider, building a different type of quantum computers. They explain about the advantage and disadvantages of various platforms and present a wealth of associated performance parameters.
However, instead of becoming more enlightened, the business owner has become more confused. He feels he has to become a quantum expert in order to follow the discussion. And it is not clear to him which quantum computer, if any, can solve his business problem.
The need for intuitive benchmarks
As quantum computing matures for business use-cases the scenario above becomes increasingly relevant. As a consequence, quantum computing benchmarks becomes a trade also for non-experts.
For the experts, it will always be relevant to compare coherence times and other component level metrics. But we should supplement these performance parameters with a metric that is both holistic and intuitive.
The number of qubits in a quantum computer is intuitive. That is probably why, when the media started to report on the first quantum computers a decade ago, a lot of emphasis was put on the number of qubits. However, it does not say anything about the quality of the qubits or the various other factors that play into the overall performance.
A different approach is to consider how well the quantum computer solves a given problem. This is known as algorithm benchmarking, and it is a much more holistic approach as it does not consider how the quantum computer operates under the hood. The trick is to pick a suitable algorithm for benchmarking.
The effective qubit number
At Kvantify we are interested in developing intuitive algorithmic benchmarks for quantum computers. To that end, we supervised a master’s thesis by a student from Aarhus University, who successfully defended his work in the summer of 2024.
The idea was to pick the quantum phase estimation (QPE) algorithm as the choice of benchmarking algorithm. This QPE algorithm is a well-known and fundamental algorithm with quantum advantage. It is representative of many actual business applications of quantum computing.
Without going into the details, the algorithm is given an input that depends on some number called the “phase”. The algorithm does its quantum thing and returns the best estimate of the value of the phase. In real applications, we do not know the value of the phase, but for our benchmarking purposes we choose the value, and can thus determine how well the QPE algorithm performs.
The QPE algorithm can be implemented for any number of qubits. The more qubits we use, the better is the produced estimate. So adding more qubits will increase the performance of the QPE algorithm, right? In principle yes, but not in practice.
Actual quantum computers are noisy, and therefore adding more qubits comes with a price tag. Think of it as an orchestra of amateurs, where a couple of players can synchronize with each other to play a melody. But adding too many becomes overwhelming, it spoils the harmony and the melody drowns in noise. In the same way, adding qubits also adds some disharmony to the overall performance budget.
Thus, when we add an extra qubit to the problem there are two combatting forces: The algorithmic gain versus the additional hardware noise. For a few qubits the algorithmic gain is expected to win, and the overall performance should increase with the number of qubits. However, as more and more qubits are introduced, the system noise is expected to take over and eventually drown everything in random noise.
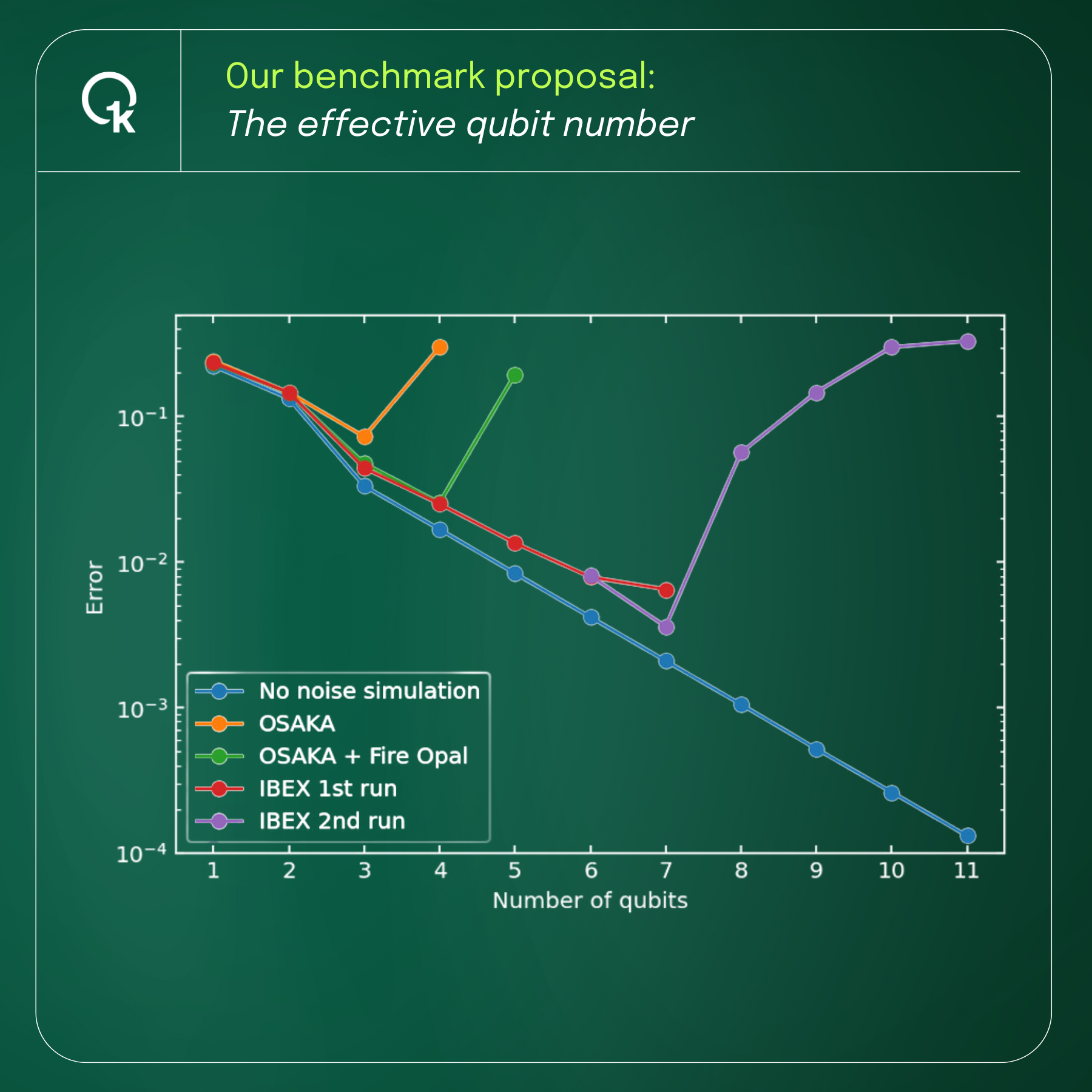
At some qubit number the performance must be optimal. This is where the difference between the estimated phase and target phase is minimal. We call this the effective qubit number.
At the effective qubit number is where you get the most out of the quantum computer running the QPE algorithm. While the quantum computer might have a lot more qubits available, the effective qubit number is, in some sense, the maximum of qubits that makes sense to utilize.
The effective qubit number attempts to find the business relevant middle ground between the number of logical and physical qubits. It is relatively simple to understand, cost-efficient to determine and a holistic benchmark that is applicable for all gate-based quantum computers.
Results and future work
As a part of the master’s thesis, two different quantum computers were benchmarked using the effective qubit number (see the figure). Firstly, the freely available superconducting quantum computer, Osaka, from IBM was found to have an effective qubit number of 3. Optimizing the quantum circuit using Fire Opal from Q-CTRL increased the performance to an effective qubit number of 4.
Secondly, in collaboration with Alpine Quantum Technologies, the IBEX quantum computer based on trapped ions was investigated. This machine was benchmarked to an effective qubit number of 7.
In both cases, the effective qubit number is clearly visible in the data.
Let’s go back to the business owner. In this case, the quantum software provider tells him that his problem shares some key aspects of the QPE problem. Thus, the effective qubit number is a relevant parameter for him. Comparing the numbers, he has a clear idea of what hardware to pick, and what to expect from it.
While the benchmark is valuable already today, Kvantify is continuing the project with a new master student from Aarhus University to further improve and generalize the method.